「高校の数学で習う〈統計〉って実際何に役立つの?」「金融や投資には興味があるけど計算が難しそう…」――そんな疑問に対して、数学B「確率分布と統計的な推測」分野の知識で求めることができる、金融や投資に関する具体的な計算方法を紹介します。
もし統計分野に苦手意識があるといった場合でも、今まで気づかなかった面白さを発見できるかもしれません!
1. はじめに
数学Bの「確率分布と統計的な推測」分野で学ぶ、「期待値」や「標準偏差」「共分散」「相関係数」などは、実は投資の世界でも用いられています。
上手に活用すればリターンやリスクの大きさもあらかじめ計算できてしまいますよ。
統計がお金の世界でどのように使われているのか、楽しく見ていきましょう。
2. 確率変数を用いた株価の計算
簡単に数学Bの内容を復習すると、「確率変数」とは試行の結果を数値で表す関数のことです。
例えば、株価が上がるか下がるかを知りたい時は、確率変数Xについて「上がる時は1」「下がる時は0」などと表すことができます。
2-1. 株価の期待収益率
確率変数を用いて株価の「期待収益率」を求めてみましょう。
「期待収益率」とは、投資などの資産運用によって期待できるリターン(獲得利益)の平均値を指します。
確率変数Xにおいて期待値E[X]は、「実現値 × 実現値の生起確率(その事象が起こる確率) の総和」で求めることができます。
確率変数の期待値とは、その確率分布に基づく平均値のようなものです。
例えば、5%の確率で1万円が当たるくじがあったとします。この時の期待値は「10,000×0.05=500」となります。
平均値との違いとしては、平均値は複数回の試行の結果から平均を求めるのに対し、期待値は「これくらいの結果が得られそうだ」という期待を表している数値と捉えましょう。
さて、この公式は、株価の収益率の期待値を求める際にも利用することができます。
例えば、A社の株価の収益率と確率がそれぞれ以下のようであると仮定します。
| 収益率 | 確率 |
|---|---|
| 10% | 0.4 |
| 0% | 0.3 |
| -15% | 0.3 |
この場合、A社株の収益率の期待値は「10×0.4+0×0.3-15×0.3=-0.5%」の式で求めることができます。
期待値がマイナスになってしまうので、ちょっとこの会社の株は買わない方が良さそうですね。
2-2. 収益率の標準偏差
期待収益率と同様に、「収益率の標準偏差」を求めてみましょう。
そもそも標準偏差とは、各データの値とそれらの平均値(期待値)からの差を表したものです。すなわち収益率の標準偏差とは投資における価格の変動幅を意味しています。
例えば、A社の株価の収益率と確率、期待値がそれぞれ以下の通りだったとします。
| 収益率 | 確率 |
|---|---|
| 10% | 0.4 |
| 0% | 0.3 |
| -15% | 0.3 |
★収益率の期待値=-0.5%
標準偏差の公式は (各値-期待値)2の総和の平方根 です。
この公式を使ってA社の株価について収益率の標準偏差を求めると、以下のようになります。
{(10+0.5)2+(0+0.5)2+(-15+0.5)2}1/2≒17.9%
平方根・累乗根の計算はやや難しいですが、関数電卓やExcelなどの表計算ソフトを使えば簡単に求めることができます。
なお、大学の定期試験では電卓持ち込み可という場合もありますよ!
3. 投資におけるポートフォリオの計算
投資における「ポートフォリオ」とは資産構成の組み合わせやその配分比率のことを指しています。組み合わせなので、「多変量確率変数」(注:複数の確率変数をまとめて扱うもの)を使って計算をします。
3-1. 2変量変数の収益率の期待値
2変量確率変数、XとYの期待値において、次の関係が成り立ちます。
E[aX+bY]=aE[X]+bE[Y]
この公式を用いて、例えば「A社とB社の株を30%と70%の割合で保有している場合」のポートフォリオについて収益率の期待値を求めてみましょう。
A社とB社の収益率の期待値と標準偏差が、それぞれ以下の通りだったとします。
・A社の収益率の期待値:-1.5%
・B社の収益率の期待値:3%
この時、A社とB社に投資するポートフォリオの期待収益率は以下の通りとなります。
0.3×(-1.5)+0.7×3=2.55%
3-2. 相関係数
はじめにA社とB社の収益率の「共分散」を求めてみましょう。
A社とB社の収益率と収益率の期待値がそれぞれ以下のような時、共分散は次の式で求めることができます。
・A社の収益率の期待値:-1.5%
・B社の収益率の期待値:3%
(A社の収益率,B社の収益率) 確率
(10%,15%) 0.3
(0%,0%) 0.4
(-15%,-5%) 0.3
共分散
(10+1.5)×(15-3)×0.3+(0+1.5)×(0-3)×0.4+(15+1.5)×(-5-3)×0.3=72
次に「相関係数」について求めてみましょう。
相関係数は共分散をそれぞれの標準偏差で割ることで求められます。
A社とB社の収益率の標準偏差がそれぞれ以下の通りだった場合、相関係数は次の式で求められます。
・A社の収益率の標準偏差:9.76%
・B社の収益率の標準偏差:8.12%
相関係数
72/(9.76×8.12)=0.91
A社とB社の収益率の相関係数は1に近く、正の相関を持つことが分かりました。正の相関を持つということは一方の収益率が下がれば、もう一方も下がり、一方の収益率が上がれば、もう一方も上がるという結果が得られるはずです。A社とB社は同じか近しい業種なのかもしれません。
もしA社とB社の株を所有するポートフォリオだった場合、両方の収益率が上がれば大きなリターンを得られる可能性がありますが、両方の収益率が下がるというケースもありリスクも大きくなってしまいます。
実際の投資の世界ではこの相関係数が低いポートフォリオにすることでリターンあたりのリスクを下げる方法がとられているケースがあります。一社の収益率が下がっても、その場合は別の会社の収益率が上がっているはずなので、結果として無事という考え方です。
このように、数学Bで習う「統計」の知識から、実際の生活に根付いた金融計算も可能なのです。
4. 無リスク資産とリスク資産
さて、一般的に投資にはリスクとリターンがつきものです。投資した会社が倒産してしまったり、株価が下がってしまったりということが起きるケースがあります。
このようなリスクを想定したり分析したりして、リスクを最小限に抑え企業活動を安定化させるプロセスを「リスクマネジメント」と言います。
一方で、リスクを持たない資産を「無リスク資産」と言います。例として、取引期間が1日の翌日満期となる国債などがあります。(リターンが確定的にわかる取引です)
リスク資産と無リスク資産、2つからなるポートフォリオの関係を式で表してみましょう。
この時リスクは「標準偏差」、リターンは「期待値」で表すことができます。
rf:無リスク資産収益率
E[rf]:リスク資産リターン(期待収益率)
σs:リスク資産リスク(収益率標準偏差)
E[r]:ポートフォリオリターン
σ:ポートフォオリスク
ω:リスク資産投資比率
★リスク資産:無リスク資産=ω:1-ω(ω>=0)で投資をおこなった場合
期待値の線形性 E[aX+bY]=aE[X]+bE[Y] より
E[r]=ωE[rs]+(1-ω)rf=rf+ω[E[rs]-rf] ・・・①
分散の公式より
σ={ω2×σs2+(1-ω)2×0+2ω(1-ω)×0}1/2=ωσs・・・②
①と②を用いてωを消去すると
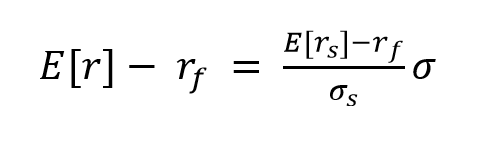
以上のような関係式が導き出せます。
このポートフォリオのリスクとリターンの関係式は次のようなグラフで表すことができます。
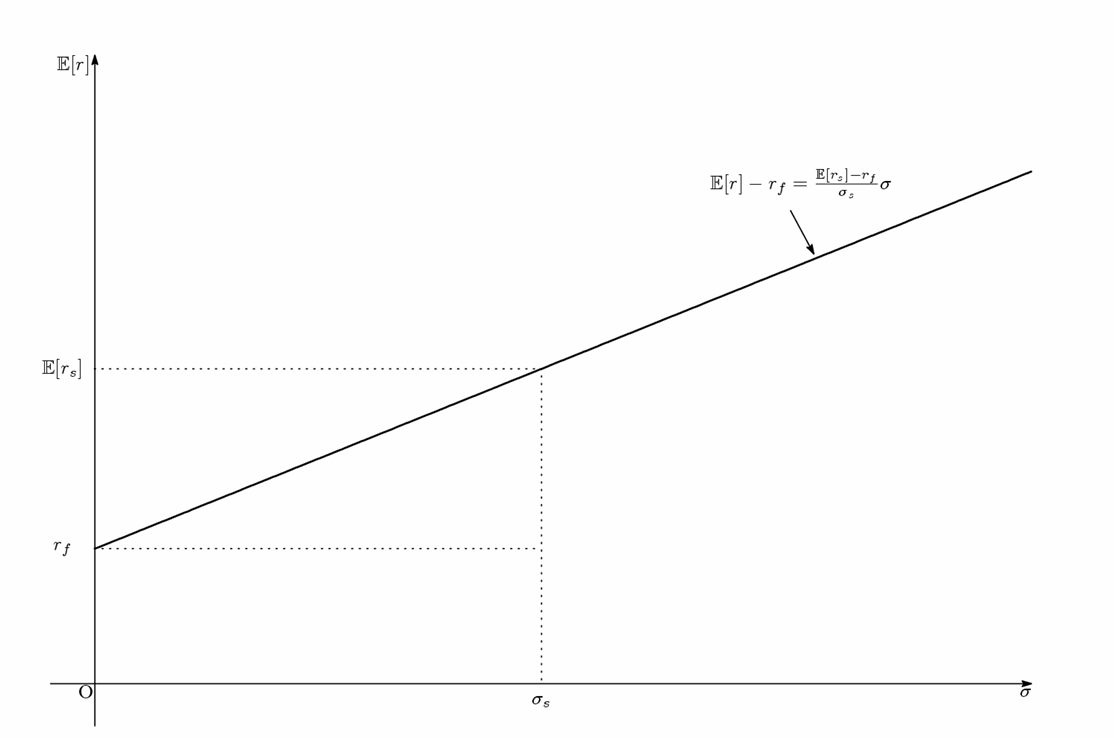
横軸がリスク、縦軸がリターンとなり、
(E[rs]-rf)/σs で表される傾きが大きくなればなるほど得られるリターンが高くなります。
点(0,rf) は無リスク資産を表し、点(σs,E[rs]) はリスク資産を表しています。
このようにグラフで表しながら他のポートフォリオとの比較などをおこない、投資における判断材料にするといった具合です。
5. 大学における「統計」の学び
大学の経営学部などで新しく学ぶ、「統計」分野の内容を紹介します。
大学での「統計学」は高校数学の延長線上で、数学Bの「統計的な推測」を発展させるようなイメージです。
大学で新しく学ぶ統計分野の例として「検定」があります。検定では仮説を立て、計算結果を出し、仮説が正しいかを確かめます。
計算結果を出す時には「背理法」を用います。背理法とは、ある命題を否定する仮説を立て、その仮説の矛盾を示すことによって、命題が真であることを証明する方法です。
検定で用いられる仮説として「帰無仮説」と「対立仮説」という考え方があります。帰無仮説と対立仮説は互いに排他的であり、ある仮説が真であれば、もう一方の仮説は偽となります。帰無仮説は通常、調査や実験において「何も起こっていない」「効果がない」「差がない」という状態を示す仮説であり、対立仮説は帰無仮説に対する仮説として本来証明したい仮説が立てられます。
例えば、ある学校が新しい教育プログラムを導入し、このプログラムが生徒の数学の成績向上に効果があるかどうかを検証するとします。この時、帰無仮説と対立仮説は以下のようになります。
・帰無仮説:新しい教育プログラムは生徒の数学の成績に対して効果がない
・対立仮説:新しい教育プログラムは生徒の数学の成績に対して効果がある
帰無仮説と対立仮説を立てたら、実際にその教育プログラムを受けた生徒とそうでない生徒の数学の成績データなどを集め、帰無仮説を検証します。検定の結果、帰無仮説が棄却されるかを判断します。
検定ではデータを標準化し「正規分布」を使って検証します。正規分布の面積が1であることや左右対称であることを利用し、仮説が示す確率が正規分布においてどれくらいの確率なのかを調べます。
背理法や正規分布などは高校数学で習う範囲なので、きちんと理解しておくと大学での学びがスムーズになるでしょう。
6. まとめ
数学B「確率分布と統計的な推測」の知識を用いて、投資にまつわる考え方や計算方法を紹介しました。
統計分野は初めこそとっつきにくい部分があるかもしれませんが、実際に使われているシーンを知ったり、具体例で学んだりすると、おもしろさが増す分野だと思います。
大学入学後、例えば経営学部などでもファイナンスや金融数学の授業で、このような計算がたびたび登場します。工学部や理工学部の金融工学系だけでなく、経営学部や経済学部など文系・理系問わず、データ分析や統計学を学ぶ機会は増えてきていますので、「数学を使って何かをしたい」「統計分野が好きになった・興味が湧いてきた」という気持ちがあれば、ぜひ大学での学びにも繋げてみてください!






















